Multiphysics Simulations, Rutgers University
Fall 2018
Skills
Computer: ANSYS (FLUENT), MATLAB, Excel
Language: Technical Writing
Team
Independent Final Project
Deliverables
Technical Report found on the Resume and Reports page
Project Summary
2D CFD in FLUENT 12.1 of mixing in a continuous supercritical hydrothermal reactor’s T-junction was conducted for varying supercritical and room temperature water directions and flow rate using linearly approximated thermophysical properties of water. The thermal and flow fields from the simulations were investigated and compared to previous 3D CFD research of the junction under similar conditions. It was revealed that the 2D simulations resulted in drastically different flow fields, and therefore thermal fields, than previous work. Unlike previous simulations, the 2D CFD simplifications were not supported by experimental results, meaning alternative routes of simplification must be investigated when modeling the junction.
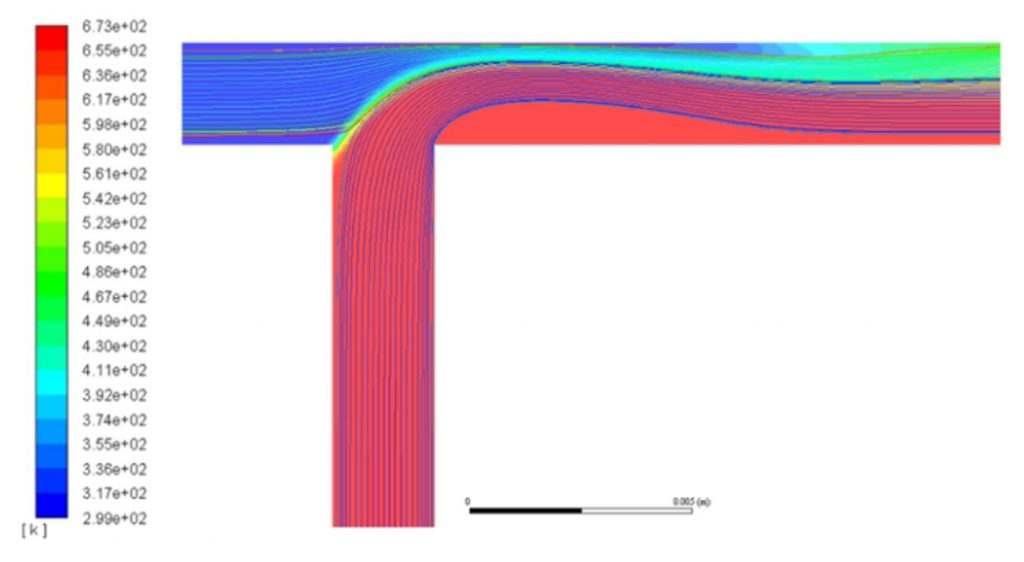
Streamlines plotted over temperature contours when cold water enters from the left and supercritical water enters from the bottom of the T junction.
Background
Nanotechnology has increasingly become the focus of modern technologies, due to their property enhancement from their high surface to bulk ratio. For instance, metal oxide nanoparticles have been the subject of catalysis, photo-catalysis, electronics, thin films, inks, and separations application research. However, the synthesis of these novel materials has continually been a limiting factor in their development. Currently, synthesis schemes such as sol gel, electrolysis, reverse-micelle, and thermal decomposition are utilized, but face issues of precursor cost, organic solvent environmental concerns, complex and lengthy synthesis schemes, and scalability of batch processing. Furthermore, high crystallinity, and controllable particle size and size distributions are of issue.
One promising alternative metal oxide nanoparticle synthesis route that circumvents these issues is continuous supercritical hydrothermal synthesis, since it only requires water and salt solution as precursors, involves relatively few components, and is continuous and therefore scalable. Supercritical synthesis in general offers distinct advantages to traditional hydrothermal methods, since beyond its critical point (p > 22.0640 MPa and T > 647.096 K) water becomes a low dielectric constant fluid with low dehydrated product solubility and an increased ion (H+ and OH-) concentration. The increased OH- ions are utilized in a two-step hydrolysis then dehydration reaction to produce metal oxide nanoparticles when supercritical water is mixed with precursor solution.
Hydrolysis: MLx + xOH– → M(OH)x + xL–
Dehydration: M(OH)x → MOx/2 + x/2H2O
Dehydration occurs on the outer surface of the hydrous products, causing smaller particles to have a higher dehydration rate and an overall rapid reaction rate.
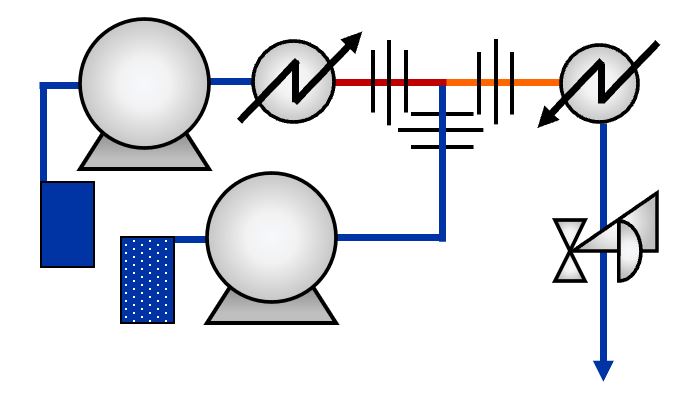
A simplified continuous supercritical hydrothermal synthesis system. Supercrtical water enters from the left and precursor solution from the bottom.
Rapid heating is used in continuous supercritical synthesis by violently mixing precursor fluid at ambient temperatures with supercritical water to reach a supercritical state. This form of heating favors nanoparticle synthesis by promoting sudden and uniform nucleation, and limits growth by avoiding temperatures gradients and quickly precipitating new particles. Although continuous supercritical hydrothermal synthesis offers key advantages to nanoparticle synthesis, the T-junction where mixing ours often faces issues of unwanted mixing patterns and blockage. Therefore, understanding flow and thermal fields at the junction is a current focus of research. Previous work has included studying these fields experimentally through neutron radiography and numerically through 3D computational fluid dynamics (CFD). While informative, these CFD studies are computationally demanding and are often undoable by student softwares and lower power computers. Therefore, in this study, the junction’s conditions for varying supercritical and ambient temperature water flows were studied using 2D FLUENT CFD analysis and simplified water properties’ temperature dependence.
Methods
The simulations were assumed to occur at 30 MPa to ensure supercritical conditions from pressure’s perspective and the existence of only two phases, liquid and supercritical water. Accordingly, the temperature dependence of water’s density, heat capacity, and thermal conductivity at 30 MPa were collected from the National Institute of Standards and Technology (NIST) Chemistry WebBook at 0.5 K increments. In order to simplify the polynomial dependence of these properties, each property was estimated as a collection of upwards to four continuous piecewise linear functions between 273.16 K and 700 K. Estimations were made by first assuming a break in the piecewise function at the temperature closest to the critical point in the NIST data, 647.36 K. Then the supercritical region was either closely estimated as a single linear region or two linear approximations split at the maximum value. The subcritical temperature region was approximated by sweeping between one or two split points, weighting each region’s R-squared value with the size of region, averaging the R-squared values for the set of split points, and determining the split points that resulted in the greatest average weighted R-squared value.
The Union T-Junction flow simulations using three configurations of supercritical water and room temperature water inlet directions were conducted using ANSYS FLUENT 12.1 software. Several starting mass flow rates ratios between room temperature water and supercritical water were tested, including experimentally tested flows. The Union T-junction was modeled after Swagelok’s SS316 1/8-inch outer diameter union tee and estimated to have a 2.29 mm inner diameter. Each inlet was kept at a fixed temperature; 298.77 K for ‘Room Temperature’ and 673.15 K for ‘Supercritical’ inputs. User-defined water was used instead of aqueous salt solution in the room temperature inlet because the experimental solutions were usually at low molality. The temperature dependence of the properties of water were inputted into FLUENT as a piecewise linear data set from the linear fits.
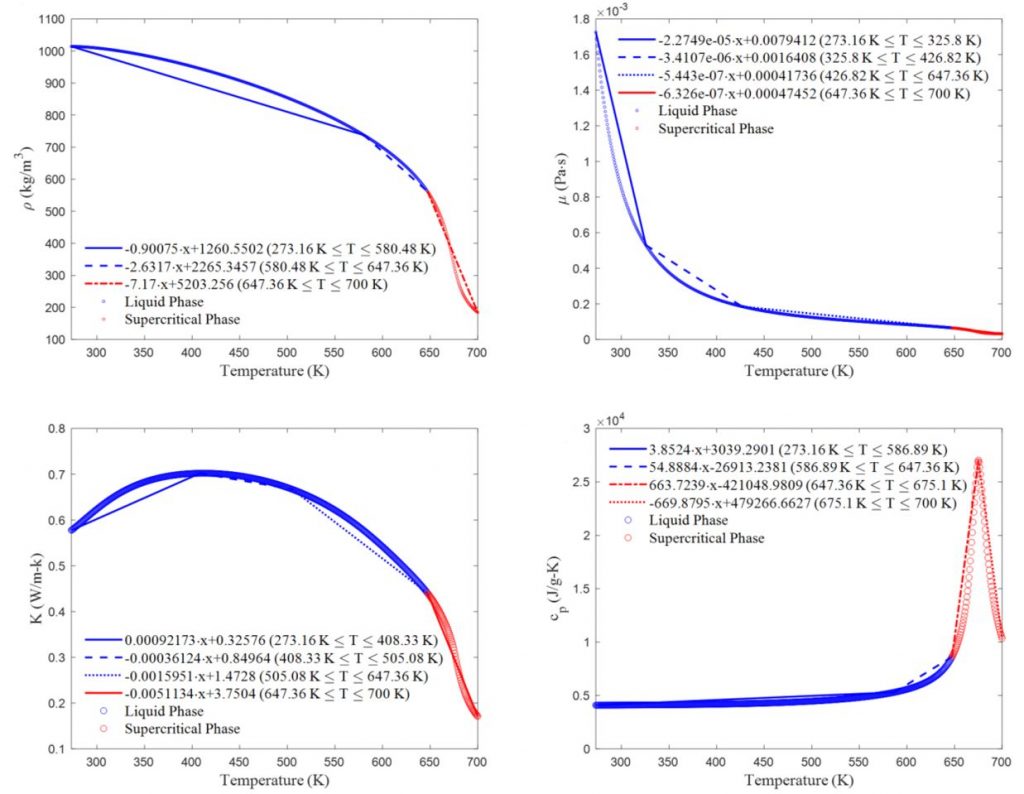
Linearly approximated isobaric thermophysical properties of water at 30 MPa.

Entry length convergence test for average and maximum outlet velocity for room temperature and supercritical water.
Convergence tests on average and maximum outlet velocities were run with for room temperature and supercritical water uniform inflows of 1 and 5 g/min, in order to achieve consistent hydrodynamic fully developed flow between simulations trials. This test’s mesh size was 1.5e-4 m and 4 inflation layers and revealed a need for 100 mm entrance length before fully developed flow. An outlet region of 47.71 mm was used to leave area for mixing.
The boundary conditions used were constant inlet velocities, and no-slip and insulating walls. Using configuration one and trails one flows, a mesh size convergence was used to determine optimal mesh size compared to computing time. There was no clear convergence at smaller mesh sizes (< 2e-4 m), however since mesh sizes below 1.5e-4 m resulted in dramatically long computation times, a mesh size of 1.5e-4 m with 4 inflation layers was implemented.
All simulations were run using the SST k-ω viscous model until convergence, which occurred below 300 iterations. All temperature and velocity calculations were conducted at steady state conditions.
Results
When compared to 3D unsteady flow simulations conducted by Sugioka et al., which revealed circulatory flow around junction corners, the flow regimes in this 2D study are drastically different.
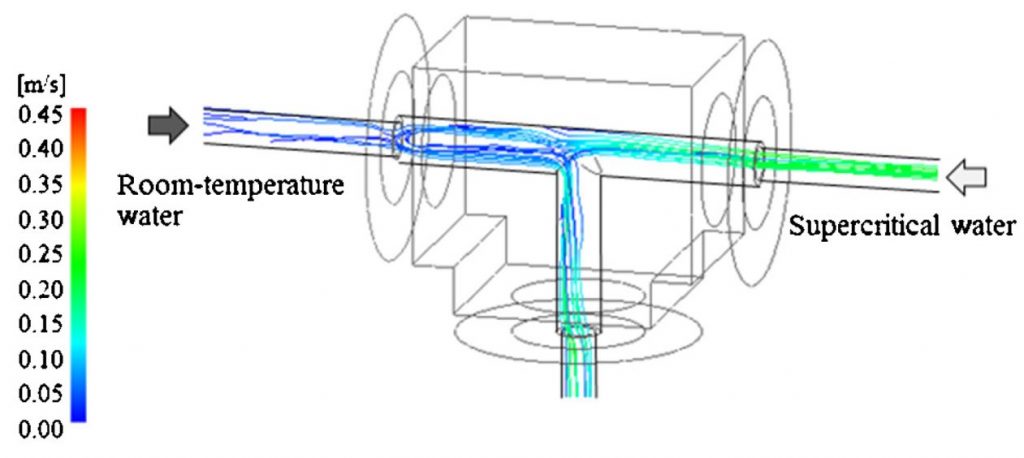
Simulated flows by Sugioka et al. clearly displaying turbulent mixing of streams.
First, all trials do not exit the simulation geometry at supercritical temperatures, highlighting inaccurate mixing or simulation set up for supercritical synthesis. Although the particle tracks demonstrate that room temperature flow is successfully flowing through the junction, there is a clear separation of flows between supercritical and room temperature water. In addition to flow separation, the particle tracks demonstrate highly laminar flow, despite the turbulent nature of these flows in small width channels. The lack of mixing is further supported by the temperature contours, since each flow contains a clear temperature gradient proportional to the distance room temperature water was in contact with the supercritical flow. If turbulent mixing were to occur such a gradient would not be as apparent, if existent at all.
Analysis of outlet velocity profiles highlights that flow separation begins to decrease as flows approach the simulation outlet. Instead of drastically differing velocity magnitudes between the upper supercritical flow and lower room temperature flow, there is an almost recovery of the parabolic profiles seen during the entry length investigation, especially at lower flow rates. Since the temperature begins to equilibrate towards the outlet, the separations may be a result of a buoyancy effect witnessed during 3D CFD studies. However, in the 2D plane and high turbulent Reynolds number flows, buoyancy driven motion should not have an effect. Further research must be conducted to fully understand the separation witnessed in these simulations.
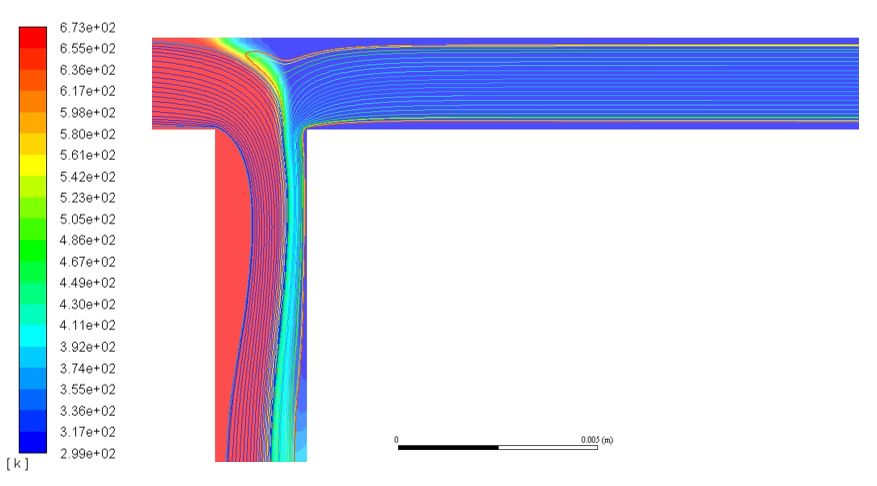
Streamlines plotted on top of temperature contours. No vortices are seen.
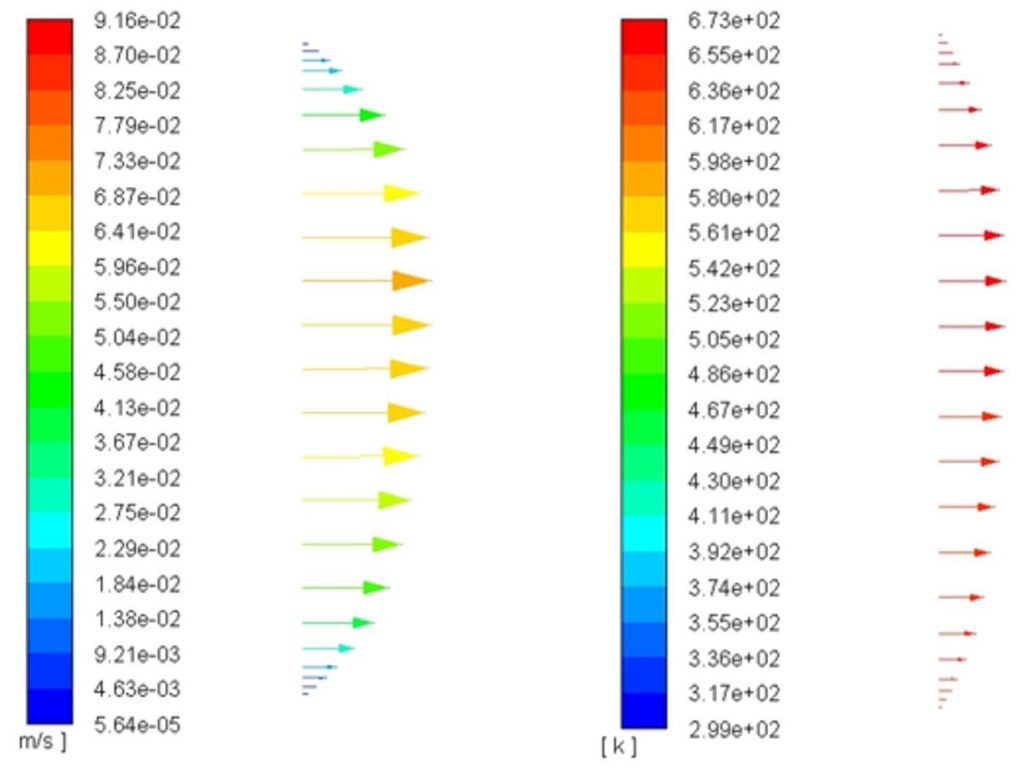
Flow and thermal profiles at the output.
The clear culprits to the different flow and thermal fields in the 2D simulations are the simplifications made. First, although less significant, are the linear approximations of water’s thermophysical properties. While the approximations will alter the flow and thermal fields dues to inaccurate values at most temperatures, they in general capture the rapid change in properties between supercritical and subcritical phases, and hence should aid in simulating relatively similar results as experimentally determined.
Therefore, the main issue is the 2D geometry itself. In a 2D simulation, mirror boundaries are implemented in and out of plane creating infinite flow channels. This not only opposes the circular pipe geometry for the T-Junction, but also restricts flow to a single plane, when turbulent flow separation usually occurs in three dimensions. These considerations, as well as the results of this study, strongly preclude the use of dimensional simplifications when modeling supercritical hydrothermal reactor junctions.